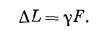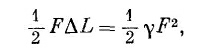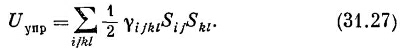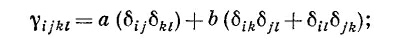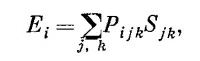| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Тензоры высших рангов
Тензор напряжений S¡j описывает внутренние силы в веществе. Если при этом материал упругий, то внутренние деформации удобно описывать с помощью другого тензора Т¡j-— так называемого тензора деформаций. Для простого объекта, подобного бруску из металла, изменение длины ΔL, как вы знаете, приблизительно пропорционально силе, т. е. он подчиняется закону Гука
Для произвольных деформаций упругого твердого тела тензор деформаций T¡j связан с тензором напряжений S¡j системой линейных уравнений
Вы знаете также, что потенциальная энергия пружины (или бруска) равна
а обобщением плотности упругой энергии для твердого тела будет выражение
Полное описание упругих свойств кристалла должно задаваться коэффициентами γijkl. Это знакомит нас с новым зверем — тензором четвертого ранга. Поскольку каждый из индексов может принимать одно из трех значений — х, у или z, то всего оказывается 34=81 коэффициент. Но различны из них на самом деле только 21. Во-первых, поскольку тензор Sij симметричен, у него остается только шесть различных величин, и поэтому в уравнении (31.27) нужны только 36 различных коэффициентов. Затем, не изменяя энергии, мы можем переставить Sij и Skl , так что γijkl должно быть симметрично при перестановке пары индексов ij и kl. Это уменьшает число коэффициентов до 21. Итак, чтобы описать упругие свойства кристалла низшей возможной симметрии, требуется 21 упругая постоянная! Разумеется, для кристаллов с более высокой симметрией число необходимых постоянных уменьшается. Так, кубический кристалл описывается всего тремя упругими постоянными, а для изотропного вещества хватит и двух.
следовательно, чтобы описать упругие свойства материала, требуются две постоянные: а и b. Я предоставляю вам самим доказать, что для кубического кристалла требуются три такие постоянные.
где E¡— электрическое поле, a Pijk— пьезоэлектрические коэффициенты (пьезомодули), составляющие тензор. Можете ли вы сами доказать, что если у кристалла есть центр инверсии (т. е. если он инвариантен относительно замены х, у, z→ –х,–у,– z), то все его пьезоэлектрические коэффициенты равны нулю. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
© All-Физика, 2009-2025
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.