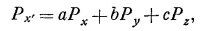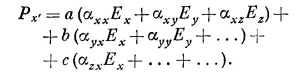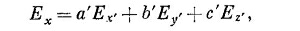Главная >> Фейнмановские лекции по физике >> Том 7 >> Глава 31. Тензоры

Преобразование компонент тензора

Вы знаете, что при замене старых осей координат новыми х′, у′ и z′ компоненты вектора Е_Х′ , Е_у′ , E_z′ тоже оказываются другими. То же самое происходит и с компонентами Р, так что для разных систем координат коэффициенты α_¡j оказываются различными. Однако вполне можно выяснить, как должны изменяться α при надлежащем изменении компонент Е и Р, ибо, если мы описываем то же самое электрическое поле, но в новой системе координат, мы должны получить ту же самую поляризацию Р. Для любой новой системы координат Р_х′ будет линейной комбинацией Р_х , Р_y ,   и P_z:

и аналогично для других компонент. Если вместо Р_х, Р_y и Р_z  подставить их выражения через Е согласно (31.4), то получится

Теперь напишите, как выражается Е_х, Е_y и Е_z через Е_х′ , Е_y′ и Е_z′ , например,

где числа а′, b′ и с′ связаны с числами а, b и с, но не равны им. Таким образом, у вас получилось выражение Р_x′ через компоненты Е_x′ , Е_y′ и E_z′ , т. е. получились новые α_¡j. Никаких хитростей здесь нет, хотя все это достаточно запутано.
 
Когда мы говорили о преобразовании осей, то считали, что положение самого кристалла фиксировано в пространстве. Если же вместе с осями поворачивать и кристалл, то α не изменяются. И обратно, если по отношению к осям изменять ориентацию кристалла, то получится новый набор коэффициентов α. Но если они известны для какой-то одной ориентации кристалла, то с помощью только что описанного преобразования их можно найти и для любой другой ориентации. Иначе говоря, диэлектрические свойства кристалла полностью описываются заданием компонент тензора поляризуемости α_¡j в любой произвольно выбранной системе координат. Точно так же как вектор скорости v = (v_x , v_y , v_z) можно связать с частицей, зная, что три его компоненты при замене осей координат будут изменяться некоторым определенным образом, тензор поляризуемости α_¡j, девять компонент которого при изменении системы осей координат преобразуются вполне определенным образом, можно связать с кристаллом.
 
Связь между Р и Е в уравнении (31.4) можно записать в более компактном виде:

где под значком i понимается какая-то из трех букв х, у или z, а суммирование ведется по j=х, у и z. Для работы с тензорами было придумано много специальных обозначений, но каждое из них удобно для ограниченного класса проблем. Одно из таких общих соглашений состоит в том, что можно не писать знака суммы (∑) в уравнении (31.5), понимая при этом, что когда один и тот же индекс встречается дважды (в нашем случае j), то нужно просуммировать по всем значениям этого индекса. Однако, поскольку работать с тензорами нам придется немного, давайте не будем осложнять себе жизнь введением каких-то специальных обозначений или соглашений.

СМОТРИТЕ ТАКЖЕ: