| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Гироскоп
Вернемся теперь снова к закону сохранения момента количества движения. Его можно продемонстрировать с помощью быстро вращающегося колеса, или гироскопа (фиг. 20.1). Если стать на крутящийся стул и держать вращающееся колесо в горизонтальном положении, то его момент количества движения будет направлен горизонтально. Момент количества движения относительно вертикальной оси нельзя изменить из-за фиксированного направления оси стула (трением пренебрегаем). Если теперь повернуть ось с колесом вертикально, то колесо приобретет момент количества движения относительно вертикальной оси. Однако система в целом (колесо, вы сами и стул) не может иметь вертикальной компоненты, поэтому вы вместе со стулом должны крутиться в направлении, обратном вращению колеса, чтобы скомпенсировать его.
Таким образом, если Ω и L0 направлены горизонтально, как это показано на фигуре, то t направлен вертикально. Чтобы уравновесить такой момент, к концам оси в горизонтальном направлении должны быть приложены силы F и —F. Откуда берутся эти силы, кто их прикладывает? Да мы сами, собственными руками, когда стараемся повернуть ось колеса в вертикальное положение. Но Третий закон Ньютона требует, чтобы равные и противоположно направленные силы (и равный, но противоположно направленный момент) действовали на нас. Они и заставляют нас крутиться вокруг вертикальной оси z в противоположном направлении.
Таким образом, если к быстро вращающемуся волчку приложить момент сил, то возникнет прецессия в направлении этого момента, т. е. под прямым углом к силам, создающим момент. Итак, теперь мы можем утверждать, что поняли прецессию гироскопа, и математически мы действительно поняли ее. Однако вся эта математика может показаться нам в каком-то смысле «колдовством». Между прочим, по мере углубления во все более сложную физику многие простые вещи легче вывести математически, чем действительно понять их фундаментальный или простой смысл. По мере того как вы будете переходить ко все более и более современным работам по физике, то обнаружите одно странное обстоятельство: математика дает результаты, которые никто не может понять непосредственно. В качестве примера можно взять уравнение Дирака, которое получается очень просто и красиво, но понять его следствия трудновато. В нашем частном случае прецессия волчка кажется чудом, каким-то тайнодействием с прямыми углами, окружностями, крутящимися силами и правовинтовыми болтами. Но давайте все-таки попытаемся понять ее физическую сущность.
До сих пор мы доказали, что, если колесо прецессирует, оно может скомпенсировать моменты сил, вызванные силой притяжения или какой-то другой причиной. Однако мы только показали, что прецессия есть одно из возможных решений уравнения. Другими словами, только при том условии, что действует момент и колесо запущено правильно, мы получим чистую прецессию. Но мы не доказали (и это вообще неверно), что чистая прецессия — наиболее общее движение вращающегося тела под действием момента сил. Общее движение включает, кроме того, какие-то колебания и отклонения от главной прецессии. Эти колебания называются нутацией. Кое-кто любит говорить, что когда на гироскоп действует момент, то он поворачивается и прецессирует, что момент сил приводит к прецессии. Кажется очень странным, что, будучи запущенным, гироскоп не падает под действием силы тяжести, а движется вбок! Как это может случиться, что направленная вниз сила тяжести, которую мы хорошо знаем и чувствуем, заставляет его двигаться вбок? Ни одна из формул в мире, подобная (20.15), не скажет нам этого, потому что формула (20.15)— это особый случай, верный только тогда, когда прецессия гироскопа уже установилась. Если же говорить о деталях, то в действительности происходит следующее. Когда мы держим гироскоп за ось, так что он никак не может прецессировать (но сохраняет свое вращение), то на него не действуют никакие моменты сил, даже момент силы тяжести, поскольку своими пальцами мы компенсируем его. Но стоит только освободить ось, как в тот же момент на нее подействует момент силы тяжести. По простоте душевной каждый решит, что конец оси должен при этом падать, и он действительно начинает падать. Это можно просто видеть, если гироскоп вращается не слишком быстро.
После того как движение устанавливается, ось гироскопа оказывается несколько ниже, чем она была вначале. Почему? (Это более сложная деталь, и мы упоминаем о ней только для того, чтобы не оставлять у читателя впечатления, что гироскоп — это чудо. Он действительно удивительная штука, но все же не чудо.) Если мы держали ось абсолютно горизонтально, а затем внезапно отпустили ее, то с помощью уравнения прецессии мы можем установить, что ось начинает прецессировать, т. е. двигаться по кругу в горизонтальной плоскости. Но это невозможно! Хотя мы и не обращали на это внимания раньше, колесо обладает каким-то моментом инерции относительно прецессирующей оси, и если оно даже медленно вращается вокруг этой оси, то оно имеет слабый момент количества движения. Отчего это происходит? Ведь если опора идеальная (т. е. если нет никакого трения), то относительно вертикальной оси никакого момента сил не может возникнуть. Тогда каким же образом прецессия все же возникает, если нет никаких моментов? Ответ: движение по циклоиде конца оси стремится к среднему стационарному движению, которое эквивалентно движению центра катящегося колеса, т. е. он устанавливается несколько ниже горизонтали. По этой причине собственный угловой момент гироскопа имеет небольшую вертикальную компоненту, которая в точности компенсирует момент количества движения прецессии. Как видите, ось должна немного опуститься, немного поддаться силе тяжести, чтобы иметь возможность крутиться вокруг вертикальной оси. Так работает гироскоп. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.


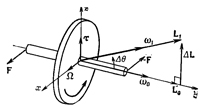 Прежде всего давайте более подробно проанализируем явление, которое мы только что описали. Самое удивительное, в чем нам следует разобраться, это откуда берутся силы, раскручивающие нас вместе со стулом, когда мы поворачиваем ось гироскопа вертикально. На фиг. 20.2 показано колесо, быстро вращающееся вокруг оси у, т. е. его угловая скорость направлена по этой оси. В ту же сторону направлен и момент количества движения. Предположим теперь, что мы хотим вращать колесо относительно оси х с малой угловой скоростью Ω; какая сила для этого требуется? Через малый промежуток времени Δt ось займет новое положение, отклонившись от горизонтального положения на угол Δθ. Поскольку основная часть момента количества движения происходит от вращения колеса (медленное вращение вокруг оси х дает очень малый вклад), мы видим, что вектор момента количества движения изменяется. Каково же изменение этого вектора? Он остается тем же самым по величине, однако направление его меняется на угол Δθ. Величина вектора ΔL поэтому равна ΔL=L0Δθ; в результате возникает момент силы, равный скорости изменения момента количества движения τ = ΔL/Δt=L0(Δθ/Δt) = L0Ω. Учитывая направление различных величин, мы видим, что
Прежде всего давайте более подробно проанализируем явление, которое мы только что описали. Самое удивительное, в чем нам следует разобраться, это откуда берутся силы, раскручивающие нас вместе со стулом, когда мы поворачиваем ось гироскопа вертикально. На фиг. 20.2 показано колесо, быстро вращающееся вокруг оси у, т. е. его угловая скорость направлена по этой оси. В ту же сторону направлен и момент количества движения. Предположим теперь, что мы хотим вращать колесо относительно оси х с малой угловой скоростью Ω; какая сила для этого требуется? Через малый промежуток времени Δt ось займет новое положение, отклонившись от горизонтального положения на угол Δθ. Поскольку основная часть момента количества движения происходит от вращения колеса (медленное вращение вокруг оси х дает очень малый вклад), мы видим, что вектор момента количества движения изменяется. Каково же изменение этого вектора? Он остается тем же самым по величине, однако направление его меняется на угол Δθ. Величина вектора ΔL поэтому равна ΔL=L0Δθ; в результате возникает момент силы, равный скорости изменения момента количества движения τ = ΔL/Δt=L0(Δθ/Δt) = L0Ω. Учитывая направление различных величин, мы видим, что 
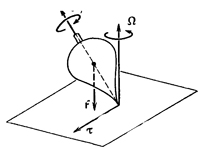 Этот результат можно обобщить на быстро вращающийся волчок. В обычном вращающемся волчке сила тяжести, действующая на его центр масс (ц. м.), создает момент относительно точки соприкосновения волчка с полом (фиг. 20.3). Этот момент действует в горизонтальном направлении и заставляет волчок прецессировать, т. е. ось его будет описывать круговой конус вокруг вертикальной оси. Если Ω — угловая скорость прецессии (направленная вертикально), то мы снова находим
Этот результат можно обобщить на быстро вращающийся волчок. В обычном вращающемся волчке сила тяжести, действующая на его центр масс (ц. м.), создает момент относительно точки соприкосновения волчка с полом (фиг. 20.3). Этот момент действует в горизонтальном направлении и заставляет волчок прецессировать, т. е. ось его будет описывать круговой конус вокруг вертикальной оси. Если Ω — угловая скорость прецессии (направленная вертикально), то мы снова находим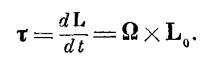
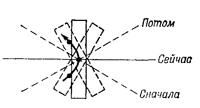 Как можно объяснить этот момент сил с помощью реально действующих сил и ускорений? Заметьте, что, когда колесо прецессирует, частицы колеса в действительности не движутся уже в одной плоскости (фиг. 20.4). Мы показали ранее (см. фиг. 19.4, стр. 80), что частица, которая пересекает ось прецессии, движется по кривому пути. Но для этого требуется какая-то боковая сила, которая возникает благодаря производимому нами давлению на ось колеса. Это давление по спицам передается частицам обода. «Постойте,— скажете вы,— а как относительно частиц на другой стороне колеса, которые движутся в обратном направлении?» Нетрудно догадаться, что действующие на них силы должны быть направлены в противоположную сторону, поэтому полная сила должна быть равна нулю. Таким образом, силы уравновешиваются, но одна из них приложена на одной стороне колеса, а другая — на другой. Эти силы можно было бы приложить непосредственно к колесу, однако из-за того, что колесо твердое, их можно приложить к оси, а через спицы они передаются на колесо.
Как можно объяснить этот момент сил с помощью реально действующих сил и ускорений? Заметьте, что, когда колесо прецессирует, частицы колеса в действительности не движутся уже в одной плоскости (фиг. 20.4). Мы показали ранее (см. фиг. 19.4, стр. 80), что частица, которая пересекает ось прецессии, движется по кривому пути. Но для этого требуется какая-то боковая сила, которая возникает благодаря производимому нами давлению на ось колеса. Это давление по спицам передается частицам обода. «Постойте,— скажете вы,— а как относительно частиц на другой стороне колеса, которые движутся в обратном направлении?» Нетрудно догадаться, что действующие на них силы должны быть направлены в противоположную сторону, поэтому полная сила должна быть равна нулю. Таким образом, силы уравновешиваются, но одна из них приложена на одной стороне колеса, а другая — на другой. Эти силы можно было бы приложить непосредственно к колесу, однако из-за того, что колесо твердое, их можно приложить к оси, а через спицы они передаются на колесо.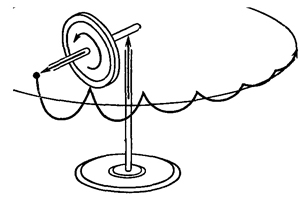 Итак, как и ожидается, конец оси гироскопа действительно начинает падать. Но поскольку он падает, то, стало быть, он вращается и тем самым создает момент сил. Это сообщает оси гироскопа движение вокруг вертикальной оси такое же, как и при постоянной прецессии. Однако вскоре скорость начинает превышать скорость при постоянной прецессии, поэтому ось начинает подниматься вверх до прежнего уровня. В результате конец оси описывает циклоиду (кривую, которую описывает камень, застрявший в шине автомобиля). Обычно это очень быстрое, незаметное для глаз движение, к тому же оно скоро затухает благодаря трению в подшипниках, а выживает только «чистая» прецессия (фиг. 20.5). Однако чем медленнее крутится колесо, тем нутация более заметна.
Итак, как и ожидается, конец оси гироскопа действительно начинает падать. Но поскольку он падает, то, стало быть, он вращается и тем самым создает момент сил. Это сообщает оси гироскопа движение вокруг вертикальной оси такое же, как и при постоянной прецессии. Однако вскоре скорость начинает превышать скорость при постоянной прецессии, поэтому ось начинает подниматься вверх до прежнего уровня. В результате конец оси описывает циклоиду (кривую, которую описывает камень, застрявший в шине автомобиля). Обычно это очень быстрое, незаметное для глаз движение, к тому же оно скоро затухает благодаря трению в подшипниках, а выживает только «чистая» прецессия (фиг. 20.5). Однако чем медленнее крутится колесо, тем нутация более заметна.