| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Кинетическая энергия вращения
Продолжим изучение динамики вращения. При обсуждении аналогии между линейным и угловым движением в гл. 18 мы использовали теорему о работе, но ничего не говорили о кинетической энергии. Какова будет кинетическая энергия твердого тела, вращающегося вокруг некоторой оси с угловой скоростью ω? Используя нашу аналогию, можно немедленно угадать правильный ответ. Момент инерции соответствует массе, угловая скорость соответствует обычной скорости, так что кинетическая энергия должна быть равна 1/2Iω2. Так оно и есть на самом деле, и сейчас мы покажем это. Предположим, что тело вращается вокруг некоторой оси, так что каждая точка движется со скоростью ωri, где ri — расстояние от данной точки до оси. Если масса этой точки равна mi, то полная кинетическая энергия всего тела равна просто сумме кинетических энергий всех частиц
В конце гл. 18 мы отмечали, что существуют очень интересные явления, связанные с вращением не абсолютно твердого тела, способного изменять свой момент инерции. Именно, в примере с вращающимся столом у нас был момент инерции I1 и угловая скорость ω1 при вытянутых руках. Согнув руки, мы изменили момент инерции до I2, а угловую скорость — до ω2. Так как у нас нет никаких моментов сил относительно оси вращения стола, то момент количества движения должен остаться постоянным. Это означает, что I1ω1 = I2ω2. А что можно сказать об энергии? Это очень интересный вопрос. Согнув руки, мы начинаем вращаться быстрее, но момент инерции при этом уменьшается и может показаться, что кинетическая энергия должна остаться той же самой. Это, однако, неверно, потому что в действительности сохраняется Iω, а не Iω2. Сравним теперь кинетические энергии в начале и в конце. В начале кинетическая энергия равна 1/2I1ω21=1/2Lω1, где L=I1ω1=I2ω2— момент количества движения. Точно таким же образом кинетическая энергия в конце равна Т=1/2Lω2, а поскольку ω2 > ω1 то кинетическая энергия в конце оказывается большей, чем в начале. Итак, вначале, когда руки были вытянуты, мы вращались с какой-то кинетической энергией, затем, согнув руки, мы стали вращаться быстрее и наша кинетическая энергия возросла. А как быть с законом сохранения энергии? Ведь должен же кто-то произвести работу, чтобы увеличить энергию? Это сделали мы сами! Но когда, в какой момент? Когда мы держим гантели горизонтально, то никакой работы не производим. Выпрямляя руки в стороны и сгибая их, мы тоже не можем произвести никакой работы. Это, однако, верно только, пока нет никакого вращения! При вращении же на гантели действует центробежная сила. Они стремятся вырваться из наших рук, так что, сгибая во время вращения руки, мы преодолеваем противодействие центробежной силы. Работа, которая на это затрачивается, и составляет разницу в кинетических энергиях вращения. Вот откуда берется этот добавок. Существует еще одно очень интересное явление, которое мы рассмотрим только описательно, чтобы просто иметь о нем представление. Хотя изучение этого явления требует несколько большего опыта, но упомянуть о нем стоит, ибо оно очень любопытно и дает много интересных эффектов. Возьмем снова эксперимент с вращающимся столиком. Рассмотрим отдельно тело и руки, с точки зрения человека, вращающегося на столике. Согнув руки с гантелями, мы стали вращаться быстрее, но заметьте, что тело при этом не изменило своего момента инерции; тем не менее оно стало вращаться быстрее, чем прежде. Если бы мы провели вокруг тела окружность и рассмотрели только предметы внутри этой окружности, то их момент количества движения изменился бы; они закрутились бы быстрее. Следовательно, когда мы сгибаем руки, на тело должен действовать момент силы. Однако центробежная сила не может дать никакого момента, так как она направлена по радиусу. Это говорит о том, что среди сил, возникающих во вращающейся системе, центробежная сила не одинока: есть еще и другая сила. Эта другая сила носит название кориолисовой силы, или силы Кориолиса. Она обладает очень странным свойством: оказывается, что если мы во вращающейся системе двигаем какой-то предмет, то она толкает его вбок. Как и центробежная сила, эта сила кажущаяся. Но если мы живем во вращающейся системе и хотим что-то двигать по радиусу, то для этого мы должны тянуть его несколько вбок. Именно эта «боковая» сила создает момент, который раскручивает наше тело. Перейдем теперь к формулам и покажем, как кориолисова сила работает на практике. Пусть Мик сидит на карусели, которая кажется ему неподвижной. С точки зрения Джо, который стоит на земле и знает истинные законы механики, карусель крутится. Предположим, что мы провели радиальную прямую на карусели и пусть Мик двигает прямо по этой линии какую-то массу. Я хочу показать, что для того, чтобы все было так, как мы описали, необходима боковая сила. Это можно увидеть, обратив внимание на момент количества движения вращающейся массы. Она крутится все время с одной и той же угловой скоростью со, поэтому ее момент количества движения равен
где через FK обозначена сила Кориолиса. В действительности мы хотели узнать, какую боковую силу должен прилагать Мик, чтобы двигать массу m со скоростью vr=dr/dt. Как видите, она равна FK = τ/r =2mωvr.
Однако с кориолисовой силой мы встречаемся не только в подобных ситуациях. Можно показать, что если предмет движется с постоянной скоростью по краю диска, то на него тоже действует кориолисова сила. Почему? Мик видит предмет движущимся со скоростью vм, а Джо видит его движущимся по окружности со скоростью vд=vм+ωr, поскольку предмет вдобавок переносится каруселью. Как мы уже знаем, действующая в этом случае сила будет, в сущности, полностью центробежной силой скорости vд, равной mv2д/r. Но, с точки зрения Мика, она должна состоять из трех частей. Все это можно записать в следующем виде:
Итак, Fr — это сила, которую измеряет Мик. Попытаемся понять, откуда что берется. Может ли Мик признать первый член? «Конечно,— сказал бы он,— даже если бы я не вращался, то такая центробежная сила должна возникнуть, если побежать по кругу со скоростью иы». Итак, это просто центробежная сила, появления которой Мик ожидает и которая не имеет ничего общего с вращением карусели. Вдобавок Мик думает, что должна быть еще одна центробежная сила, действующая даже на неподвижные предметы на его карусели. Это дает третий член. Однако в дополнение к ним существует еще один член — второй, который опять равен 2mωvМ. Раньше, при радиальной скорости, кориолисова сила FK была тангенциальна. Теперь же, при тангенциальной скорости, она радиальна. В самом деле, одно выражение отличается от другого только знаком. Сила всегда имеет одно и то же направление по отношению к скорости независимо от того, куда направлена скорость. Она действует под прямым углом к скорости и равна по величине 2mωv. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.

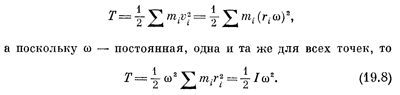
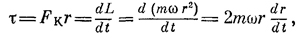
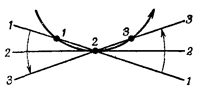 Теперь, имея формулу для кориолисовой силы, давайте рассмотрим несколько более подробно всю картину в целом. Как можно понять причину возникновения этой силы из элементарных соображений? Заметьте, что кориолисова сила не зависит от расстояния до оси и поэтому действует даже на оси! Оказывается, что легче всего понять именно силу, действующую на оси вращения. Для этого нужно просто посмотреть на все происходящее из инерциальной системы Джо, который стоит на земле. На фиг. 19.4 показаны три последовательных положения массы т, которая при t=0 проходит через ось. Из-за вращения карусели масса, как мы видим, движется не по прямой линии, а по некоторому кривому пути, касающемуся диаметра в точке r=0. Но для того чтобы она двигалась по кривому пути, должна действовать ускоряющая сила. Это и есть кориолисова сила.
Теперь, имея формулу для кориолисовой силы, давайте рассмотрим несколько более подробно всю картину в целом. Как можно понять причину возникновения этой силы из элементарных соображений? Заметьте, что кориолисова сила не зависит от расстояния до оси и поэтому действует даже на оси! Оказывается, что легче всего понять именно силу, действующую на оси вращения. Для этого нужно просто посмотреть на все происходящее из инерциальной системы Джо, который стоит на земле. На фиг. 19.4 показаны три последовательных положения массы т, которая при t=0 проходит через ось. Из-за вращения карусели масса, как мы видим, движется не по прямой линии, а по некоторому кривому пути, касающемуся диаметра в точке r=0. Но для того чтобы она двигалась по кривому пути, должна действовать ускоряющая сила. Это и есть кориолисова сила.