| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Свойства центра масс
В предыдущей главе мы установили факт существования некоторой замечательной точки, называемой центром масс. Она замечательна тем, что если на частицы, образующие тело (неважно, будет ли оно твердым или жидким, звездным скоплением или чем-то другим), действует великое множество сил (конечно, имеются в виду только внешние силы, поскольку все внутренние силы компенсируют друг друга), то результирующая сила приводит к такому ускорению этой точки, как будто в ней сосредоточена вся масса тела М. Давайте теперь обсудим свойство центра масс несколько подробнее. Положение центра масс (сокращенно ц. м.) определяется уравнением
Это, разумеется, векторное уравнение, т. е. фактически три уравнения — по одному для каждого из трех направлений. Но мы будем рассматривать только х-направление; если вы поймете, что происходит в ж-направлении, то поймете и два остальных. Что означает равенство Xц.м. = Σmixi/Σmi?Предположим на минуту, что тело разделено на маленькие кусочки с одинаковой массой т, причем полная масса будет равна числу таких кусочков N, умноженному на массу одного кусочка, скажем 1 г, или какую-то другую единицу. Тогда наше уравнение просто означает, что нужно взять координаты х всех кусочков, сложить их и результат разделить на число кусочков, т. е. Xц.м. = mΣxi/mN = Σxi/N. Иными словами, если массы кусочков равны, то Xц.м. будет просто средним арифметическим x-координат всех кусочков. Но предположим, что один из кусочков вдвое тяжелее, чем каждый из остальных. Тогда в нашу формулу его координата будет входить с коэффициентом 2, т. е. в суммах ее нужно учитывать дважды. Нетрудно понять, почему это происходит. Ведь тяжелый кусочек можно представить себе как бы состоящим из двух легких, таких же, как и все остальные, так что, когда мы вычисляем среднее, его координату х нужно учитывать дважды: ведь кусочков-то в этом месте два. Таким образом, Xц.м. равно просто среднему арифметическому x-координат всех масс, причем каждая координата считается некоторое число раз, пропорциональное массе, как будто она разделена на маленькие кусочки единичной массы. Исходя из этого, легко доказать, что Xц.м. должна находиться где-то между самой близкой и самой далекой частичкой. Вообще центр масс должен лежать где-то внутри многогранника, проведенного через крайние точки тела. Однако вовсе не обязательно, чтобы центр масс находился в самом теле; ведь могут быть тела, подобные окружности, например обруч, центр масс которого находится в геометрическом центре, а не на самом обруче. Конечно, если объект симметричен, например прямоугольник, обладающий линией симметрии, то его центр масс должен лежать где-то на этой линии. Кстати, прямоугольник имеет еще одну линию симметрии и это однозначно определяет положение его центра масс. Для просто симметричного объекта центр масс должен лежать где-то на оси симметрии! ведь отрицательных х в этом случае ровно столько же, сколько и положительных.
Пусть мы хотим определить центр масс сложного тела, одни из частиц которого принадлежат части А, а другие — части В. При этом мы можем разбить полную сумму Σmixi на сумму по части А, т. е. ΣAmixi и сумму по части В, т. е. ΣВmixi. Если бы мы находили центр масс только части А, то нам потребовалась бы первая из этих сумм, которая, как вы знаете, равна МАХА, т. е. полной массе части А на х-координату ее центра масс: это просто следствие теоремы о центре масс, примененной к части А. То же самое можно сказать и о части В. Сумма ΣВmixi должна быть равна МВХВ. Сложив эти два результата, мы, конечно, должны получить MX, т. е.
Полная же масса М,очевидно, равна МА + МВ, так что выражение (19.2) представляет собой не что иное, как определение центра масс двух точек, одна из которых имеет массу МА и координату ХА, а другая — массу МВ и координату ХВ. Теорема о движении центра масс интересна не только сама по себе, она еще играет очень важную роль в развитии нашего понимания физики. Если мы предположим, что законы Ньютона верны только для маленьких частей, составляющих большое тело, то эта теорема показывает, что они верны также и для большого тела. Мы можем не знать его детального строения и нам известны лишь общая масса и полная сила, действующая на него. Другими словами, законы Ньютона имеют ту особенность, что если они справедливы в малом масштабе, то справедливы и в большом. Нет никакой нужды рассматривать футбольный мяч как ужасно сложную вещь, состоящую из мириада взаимодействующих частиц, а достаточно изучить только движение его центра масс под действием внешней силы F, чтобы получить F=ma, где а — ускорение центра масс, a m — полная масса мяча. Итак, закон F=ma воспроизводит сам себя в большом масштабе. (Наверное, должно быть какое-нибудь хорошее греческое слово, которым можно было бы назвать подобные воспроизводящие себя в большом масштабе законы.) Нетрудно, конечно, догадаться, что первый открытый человеком закон должен быть именно таким законом, воспроизводящим самого себя в большом масштабе. Почему? Да просто потому, что истинный размер фундаментальных «винтиков и колесиков» Вселенной есть атомный размер, который настолько меньше размеров окружающих нас вещей, что только сейчас начинает входить в обычную жизнь. Итак, первая открытая человеком закономерность не могла иметь отношения к размерам атомного масштаба. Если бы законы для малых частиц не воспроизводили себя в большом масштабе, то открыть их было бы не так-то легко. А что можно сказать об обратной проблеме? Должны ли законы микромира быть теми же самыми, что и для больших тел? Никакой необходимости в этом, конечно, нет. Давайте, однако, предположим, что истинное движение атомов описывается неким странным уравнением, которое не воспроизводит себя при переходе к большему масштабу. Вместо этого оно обладает тем свойством, что при таком переходе его можно приближенно заменить каким-то выражением, которое при все большем и большем увеличении масштаба воспроизводит само себя. Это вполне может случиться, и в действительности так оно и происходит. Законы Ньютона являются как бы «кончиком хвоста» атомных законов, продолженных до очень больших размеров. Истинные законы движения частиц очень малых размеров весьма специфичны, но если мы возьмем большое число частиц и скомбинируем законы их движения, то приближенно, и только приближенно, получим законы Ньютона. После этого законы Ньютона позволяют нам двигаться ко все большим размерам, оставаясь при этом теми же самыми законами. В сущности, при переходе ко все большим и большим размерам они все точнее и точнее описывают природу. Так что факт самовоспроизводимости законов Ньютона — отнюдь не фундаментальное свойство природы, а важная историческая особенность. Основываясь на своих первых наблюдениях, мы никоим образом не смогли бы открыть фундаментальные атомные законы, поскольку наблюдения эти были слишком грубыми. Действительно, фундаментальные атомные законы, которые мы называем квантовой механикой, так сильно отличаются от законов Ньютона, что понять их не просто. Ведь у нас есть только опыт обращения с телами больших размеров, а крохотные атомы ведут себя совершенно невиданным для таких тел образом. Мы не можем сказать: «Электроны в атомах напоминают планеты, крутящиеся вокруг Солнца», или что-то в этом роде. Они не похожи ни на что известное нам, ибо мы не видим ничего похожего на них. Если мы применяем квантовую механику ко все большим и большим объектам, то законы поведения такого коллектива атомов не воспроизводят поведения одного атома, а дают новый закон— закон Ньютона, который уже воспроизводит сам себя, начиная с объектов весом в 1 миллионную микрограмма, содержащих еще миллиарды и миллиарды атомов, и вплоть до тел величиной с Землю и даже еще больших. Вернемся, однако, к центру масс. Часто его называют центром тяжести, так как во многих случаях для силы тяготения можно провести точно такие же рассуждения, как и для масс. Если размеры достаточно малы, то силу тяжести можно считать не только пропорциональной массе, но и направленной всюду параллельно некоторой фиксированной линии. Возьмем тело, в котором сила тяжести действует на каждую из составляющих его частей, a mi — масса одной из этих частей. Действующая на нее сила тяжести будет тогда равна произведению mi на g. Возникает вопрос: в какой точке нужно приложить одну-единственную силу, чтобы сбалансировать притяжение всего тела так, чтобы оно (если это твердое тело) не вращалось? Ответ: сила должна проходить через центр масс. Доказывается это следующим образом. Чтобы тело не вращалось, сумма моментов всех сил должна быть равна нулю, ибо если нет момента сил, то нет и изменения момента количества движения, а поэтому нет и вращения. Таким образом, мы должны подсчитать сумму всех моментов, действующих на все частицы, и посмотреть, какой получится полный момент относительно любой данной оси: он должен быть равен нулю, если ось проходит через центр масс. Направив ось х горизонтально, а ось у вертикально, мы найдем, что моменты сил равны силам, направленным вниз, умноженным на плечо х (т. е. сила на плечо относительно той оси, для которой измеряется момент силы). Полный же момент равен сумме
Чтобы полный момент отсутствовал, сумма Σmixi должна быть равна нулю. Но эта сумма равна MX — полной массе, умноженной на расстояние от оси х до центра масс. Итак, это расстояние должно быть равно нулю. Разумеется, мы провели проверку только для x-направления, однако если мы действительно взяли центр масс, то тело должно быть уравновешено в любом положении, поэтому, повернув его на 90°, мы вместо оси х получим ось у. Другими словами, если держать тело за центр масс, то параллельное гравитационное поле не дает никакого момента сил. Если же объект настолько велик, что становится существенной непараллельность сил притяжения, то точку, в которой должна быть приложена уравновешивающая сила, описать не просто: она несколько отклоняется от центра масс. Вот почему нужно помнить, что центр масс и центр тяжести — разные вещи. Тот факт, что тело, поддерживаемое точно за центр масс, уравновешено в любом положении, имеет еще одно интересное следствие. Если вместо гравитационных сил взять инерционные псевдосилы, возникающие вследствие ускорения, то, чтобы найти точку, уцепившись за которую мы уравновесим все моменты этих сил, можно использовать ту же самую математическую процедуру. Предположим, что мы заключили тело внутрь ящика, который ускоряется вместе со всем его содержимым. Тогда, с точки зрения наблюдателя, сидящего в этом ящике, на тело вследствие инерции будет действовать некая эффективная сила. Иначе говоря, чтобы заставить тело двигаться вместе с ящиком, нужно подталкивать и ускорять его. Эта сила «уравновешивается силой инерции», которая равна массе тела, умноженной на ускорение ящика. Наблюдателю в ящике будет казаться, будто тело находится в однородном гравитационном поле, величина g которого равна ускорению ящика α. Таким образом, инерционные силы, возникающие вследствие ускорения тела, не имеют момента относительно центра масс. Этот факт имеет очень интересное следствие. В инерционной системе, движущейся без ускорения, момент сил всегда равен скорости изменения момента количества движения. Однако равенство момента силы и скорости изменения момента количества движения остается справедливым даже для ускоряющегося тела, если взять ось, проходящую через центр масс. Таким образом, теорема о равенстве момента сил скорости изменения момента количества движения верна в двух случаях; 1) ось фиксирована — в инерциальной системе; 2) ось проходит через центр масс — даже когда тело ускоряется. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.

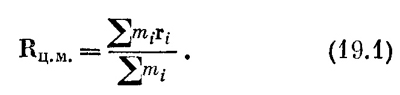
 Существует еще один очень забавный способ нахождения центра масс. Вообразите себе тело, состоящее из двух кусков А и В (фиг. 19.1). Центр масс в этом случае можно найти следующим образом. Находим сначала отдельно центры масс составных частей А и В и их полные массы МА и МВ. После этого находим центр масс двух точечных тел, одно из которых имеет массу МА и расположено в центре масс части А, а другое — массу МВ и расположено в центре масс части В. Полученная точка и будет центром масс всего тела. Другими словами, если нам известны центры масс всех частей сложного тела, то, чтобы найти его центр масс, не нужно повторять все сначала, а достаточно просто найти центр масс системы точечных тел с массами, равными массам каждой из частей и расположенными в их центрах масс. Посмотрим, как это получается.
Существует еще один очень забавный способ нахождения центра масс. Вообразите себе тело, состоящее из двух кусков А и В (фиг. 19.1). Центр масс в этом случае можно найти следующим образом. Находим сначала отдельно центры масс составных частей А и В и их полные массы МА и МВ. После этого находим центр масс двух точечных тел, одно из которых имеет массу МА и расположено в центре масс части А, а другое — массу МВ и расположено в центре масс части В. Полученная точка и будет центром масс всего тела. Другими словами, если нам известны центры масс всех частей сложного тела, то, чтобы найти его центр масс, не нужно повторять все сначала, а достаточно просто найти центр масс системы точечных тел с массами, равными массам каждой из частей и расположенными в их центрах масс. Посмотрим, как это получается.