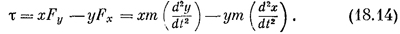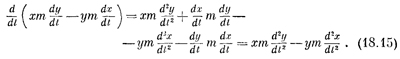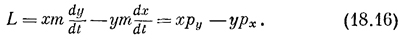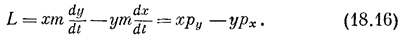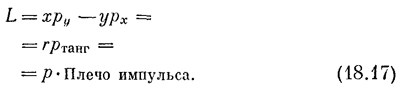| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Момент количества движения
Хотя до сих пор мы рассматривали только специальный случай твердого тела, свойства момента и его математическое выражение интересны даже тогда, когда тело не твердое. Можно доказать очень интересную теорему: подобно тому как внешняя сила равна скорости изменения величины p, которая называется полным импульсом системы частиц, так и момент силы равен скорости изменения некоторой величины L, называемой моментом количества движения, или угловым моментом группы частиц.
Хотя сразу и не видно, что это выражение является производной от какой-то простой величины, но на самом деле оно равно производной от xm(dy/dt)—ym(dx/dt). Действительно,
Оказывается, таким образом, что момент силы равен скорости изменения со временем некоторой величины! Давайте обратим внимание на эту величину и прежде всего дадим ей имя. Она будет называться моментом количества движения, или угловым моментом, и обозначаться буквой L
Хотя во всех наших рассмотрениях мы не принимали в расчет теорию относительности, тем не менее второе выражение для L верно и при учете ее. Итак, мы нашли, что у обычного импульса также существует вращательный аналог — угловой момент, который связан с компонентами импульса точно так же, как и момент силы связан с компонентами силы! Так что если мы хотим вычислить момент количества движения относительно какой-то оси, то должны взять тангенциальную составляющую импульса и умножить ее на радиус. Другими словами, угловой момент показывает, насколько быстро движется частица вокруг какого-то центра, ведь он учитывает только тангенциальную часть импульса. Более того, чем дальше от центра удалена линия, по которой направлен импульс, тем больше будет угловой момент. Точно так же, поскольку геометрия в этом случае та же, что и в случае момента силы, существует плечо импульса (оно, разумеется, не совпадает с плечом силы, действующей на частицу), которое равно расстоянию линии импульса от оси. Таким образом, угловой момент равен просто величине импульса, умноженного на его плечо. Точно так же, как и для момента силы, для углового момента мы можем написать следующие три формулы:
Момент количества движения, как и момент силы, зависит от положения оси, относительно которой он вычисляется. Прежде чем перейти к рассмотрению более чем одной частицы, применим полученные выше результаты к движению планеты вокруг Солнца. В каком направлении действует сила? Конечно, по направлению к Солнцу. А какой при этом будет момент силы? Разумеется, все зависит от того, в каком месте мы выберем ось, однако результат получится совсем простым, если в качестве точки вращения выбрать само Солнце. Поскольку момент силы равен силе, умноженной на ее плечо, или компоненте силы, перпендикулярной к радиусу r, умноженной на r, то в этом случае нет никакой тангенциальной составляющей силы, а поэтому момент силы относительно оси, проходящей через Солнце, равен нулю. Следовательно, момент количества движения должен оставаться постоянным. Давайте-ка посмотрим, что это означает. Произведение тангенциальной компоненты скорости на массу и радиус, будучи моментом количества движения, должно оставаться постоянным, потому что скорость его изменения есть момент силы, который в нашем случае равен нулю. Это означает, что остается постоянным произведение тангенциальной компоненты скорости на радиус, поскольку масса-то уж, конечно, не изменяется. Но такая величина, характеризующая движение планеты, уже вычислялась нами раньше. Предположим, что мы взяли маленький промежуток времени At. Какое расстояние пройдет планета при своем движении из точки Р в точку Q (фиг. 18.3)? Как велика площадь той области, которую «заметает» прямая, соединяющая планету с Солнцем? Пренебрегая площадью QQ`P, которая очень мала по сравнению с OPQ, находим, что площадь этой области равна половине основания PQ, умноженного на высоту OR. Другими словами, «заметенная» площадь равна половине произведения скорости на ее плечо. Так что скорость изменения этой площади пропорциональна моменту количества движения, который остается постоянным. Итак, мы получим, что закон Кеплера о равных площадях за равные промежутки времени является просто словесным описанием закона сохранения момента количества движения, когда моменты внешних сил отсутствуют. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.

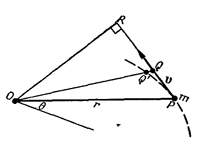 Чтобы доказать это, рассмотрим систему частиц, на которую действуют силы, и посмотрим, что произойдет с системой в результате действия вращающих моментов, созданных этими силами. Для начала давайте возьмем только одну частицу. Такая частица с массой m и осью О изображена на фиг. 18.3. Она не обязательно должна вращаться по окружности вокруг оси О, а может двигаться и по эллипсу, подобно планете вокруг Солнца, или по какой-нибудь другой кривой. Главное то, что она движется, что на нее действует сила, которая ускоряет ее в соответствии с обычными законами: x-компонента силы равна массе, умноженной на x-компоненту ускорения, и т. д. Но посмотрим теперь, как действует момент силы. Он, как вы знаете, равен xFy—yF`х, а х- и y-компоненты силы в свою очередь равны массе, умноженной соответственно на х- и y-компоненту ускорения, так что
Чтобы доказать это, рассмотрим систему частиц, на которую действуют силы, и посмотрим, что произойдет с системой в результате действия вращающих моментов, созданных этими силами. Для начала давайте возьмем только одну частицу. Такая частица с массой m и осью О изображена на фиг. 18.3. Она не обязательно должна вращаться по окружности вокруг оси О, а может двигаться и по эллипсу, подобно планете вокруг Солнца, или по какой-нибудь другой кривой. Главное то, что она движется, что на нее действует сила, которая ускоряет ее в соответствии с обычными законами: x-компонента силы равна массе, умноженной на x-компоненту ускорения, и т. д. Но посмотрим теперь, как действует момент силы. Он, как вы знаете, равен xFy—yF`х, а х- и y-компоненты силы в свою очередь равны массе, умноженной соответственно на х- и y-компоненту ускорения, так что