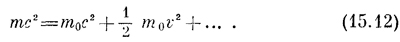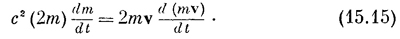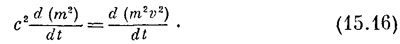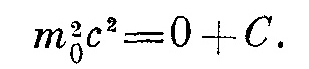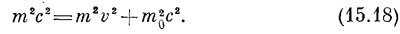| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Связь массы и энергии
Это наблюдение навело Эйнштейна на мысль, что массу тела можно выразить проще, чем по формуле (15.1), если сказать, что масса равна полному содержанию энергии в теле, деленному на с2. Если (15.11) помножить на с2, получается
Здесь левая часть дает полную энергию тела, а в последнем члене справа мы узнаем обычную кинетическую энергию. Эйнштейн осмыслил первый член справа (очень большое постоянное число m0c2) как часть полной энергии тела, а именно как его внутреннюю энергию, или «энергию покоя». К каким следствиям мы придем, если вслед за Эйнштейном предположим, что энергия тела всегда равна mс2? Тогда мы сможем вывести формулу (15.1) зависимости массы от скорости, ту самую, которую до сих пор мы принимали на веру. Пусть тело сперва покоится, обладая энергией m0с2. Затем мы прикладываем к телу силу, которая сдвигает его с места и поставляет ему кинетическую энергию; раз энергия примется возрастать, то начнет расти и масса (это все заложено в первоначальном предположении). Пока сила действует, энергия и масса продолжают расти. Мы уже видели (см. гл. 13), что быстрота роста энергии со временем равна произведению силы на скорость
Кроме того, F = d(mv)/dt [см. гл. 9, уравнение (9.1)]. Связав все это с определением Е и подставив в (15.13), получим
Мы хотим решить это уравнение относительно m. Для этого помножим обе части на 2m. Уравнение обратится в
Теперь нам нужно избавиться от производных, т. е. проинтегрировать обе части равенства. В величине (2m) dm/dt можно узнать производную по времени от m2, а в (2mv)*d(mv)/dt — производную по времени от (mv)2. Значит, (15.15) совпадает с
Когда производные двух величин равны, то сами величины могут отличаться не больше чем на константу С. Это позволяет написать
Определим теперь константу С явно. Так как уравнение (15.17) должно выполняться при любых скоростях, то можно взять v= 0 и обозначить в этом случае массу через m0. Подстановка этих чисел в (15.17) дает
Это значение С теперь можно подставить в уравнение (15.17). Оно принимает вид
Разделим на с2 и перенесем члены с m в левую часть
А это и есть формула (15.1), т. е. как раз то, что необходимо, чтобы в уравнении (15.12) было соответствие между массой и энергией. В обычных условиях изменения в энергии приводят к очень малым изменениям в массе: почти никогда не удается из данного количества вещества извлечь много энергии; но в атомной бомбе с энергией взрыва, эквивалентной 20 000 тонн тринитротолуола, весь пепел, осевший после взрыва, на 1 г легче первоначального количества расщепляющегося материала. Это потому, что выделилась энергия, которая имела массу 1 г, в согласии с формулой ΔЕ = Δ(mс2). Вывод об эквивалентности массы и энергии прекрасно подтвердился в опытах по аннигиляции материи — превращению вещества в энергию. Электрон с позитроном могут взаимодействовать в покое, имея каждый массу покоя m0. При сближении они исчезают, а вместо них излучаются два γ-луча, каждый опять с энергией m0с2. Этот опыт прямо сообщает нам о величине энергии, связанной с существованием массы покоя у частицы. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
© All-Физика, 2009-2025
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.