| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Поле тяготения больших тел
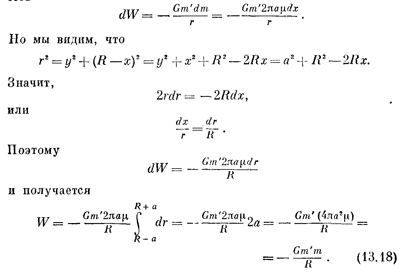
Все массы dm, которые находятся на одном и том же расстоянии rот Р, дадут одно и то же значение dCх, так что за dm можно сразу принять массу всего кольца между p и p+dp, т. е. dm=μ2πpdp (2πpdp — это площадь кольца радиусом p и шириной dp при dp << p). Итак, Но pdp= rdr из-за того, что г2 = p2+a2. Поэтому
Стало быть, сила не зависит от расстояния а! Почему? Не ошиблись ли мы? Казалось бы, чем дальше от плоскости, тем сила слабее. Но нет! Если точка находится вплотную к плоскости, то большая часть вещества притягивает ее под неудачными углами, а если вдалеке, то у большей части вещества притяжение направлено прямее к плоскости. На любом расстоянии самая «влиятельная» часть плоскости лежит в некотором конусе. С удалением сила ослабляется обратно пропорционально квадрату расстояния, но в том же конусе под тем же углом оказывается больше вещества, а рост количества вещества тоже пропорционален квадрату расстояния! Этот анализ может быть сделан более строгим, если заметить, что дифференциал вклада любого данного конуса не зависит от расстояния в результате противоположных изменений напряженности поля данной массы и количества самой этой массы (с ростом расстояния). Впрочем, на самом деле сила не постоянна, ибо на другой стороне плоскости она меняет знак. Мы решили, кстати, и задачу по электричеству: мы доказали, что у заряженной пластины, каждая единица площади которой несет заряд σ, электрическое поле равно σ/2ε0 и направлено от пластины, если она заряжена положительно, и к ней, если она заряжена отрицательно. Чтобы доказать это, надо просто вспомнить, что в законе тяготения G играет ту же роль, что 1/4πε0 в электричестве. А теперь пусть имеются две пластины, одна с положительным зарядом +σ, а другая с отрицательным —σ (на единицу площади), и пусть промежуток между ними равен D. Каково поле этих пластин? Снаружи пластин поле равно нулю. Отчего? Оттого, что одна из них отталкивает, а другая притягивает и у обеих сила не зависит от расстояния; значит, силы всюду уничтожаются! А вот поле между пластинами вдвое больше, чем поле одной пластины, направлено оно от положительной пластины к отрицательной и равно Е=σ/ε0. Перейдем теперь к еще более интересному и важному вопросу; впрочем, мы давно уже ответили на него, предположив, что сила притяжения Земли в точке на ее поверхности или над нею такая же, как если бы вся масса Земли сосредоточилась в ее центре. Справедливость этого предположения не очевидна: ведь когда мы находимся у самой земли, какая-то часть ее массы очень к нам близка, а другая далека и т. д. Когда мы складываем действие всех таких масс, то кажется чудом, что в конце концов сила сводится к тому, что вся Земля сжалась в одну точку, стянулась к своему центру!
Стало быть, для тонкого слоя потенциальная энергия массы m`, внешней по отношению к слою, такова, как если бы масса слоя собралась в его центре. Землю же можно представить в виде ряда таких слоев, и притяжение каждого из слоев зависит только от его массы; сложив их, получим всю массу планеты; значит, и вся Земля действует так, словно все ее вещество находится в ее центре! Но посмотрим, что произойдет, если точка Р окажется внутри слоя. Проделывая те же расчеты вплоть до интегрирования, мы получим разность двух значений r, но уже в другой форме: (a + R)—(а—R)=2R (двойное расстояние от Р до центра). Другими словами, теперь W становится равной W = — Gmm`/a, что не зависит от R, т. е. точка Р всюду внутри сферы обладает одной и той же энергией тяготения. А значит, на нее не действует никакая сила, и не нужно никакой работы, чтобы двигать ее внутри. Когда потенциальная энергия тела всюду, в любой точке внутри сферы, одинакова, то на тело не действует никакая сила. Внутри сферы тело не испытывает действия сил, сила действует только снаружи. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.

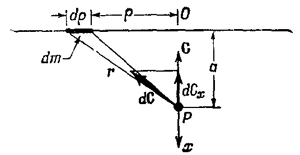 Теперь рассчитаем поля, встречающиеся во многих физических задачах, когда речь идет о распределении масс. Мы пока не рассматривали распределения масс, а занимались только отдельными частицами. Но интересно рассчитать и поля, образуемые более чем одной частицей. Для начала найдем силу притяжения со стороны плоско го пласта вещества бесконечнойпротяженности. Сила притяжения единичной массы в данной точке Р (фиг. 13.5), конечно, направлена к плоскости. Расстояние от точки до плоскости есть а, а масса единицы площади этой плоскости есть μ. Пусть |х будет постоянной: слой однороден. Какой же величины поле dC создается массой dm, удаленной от О не ближе, чем на p, и не дальше, чем на p+ dp (О — это точка плоскости, ближайшая к Р)? Ответ: dC = G(dmr/r3). Но оно, это поле, направлено вдоль r, а мы понимаем, что из трех составляющих С после сложения всех dC должна остаться лишь x-составляющая. Она равна
Теперь рассчитаем поля, встречающиеся во многих физических задачах, когда речь идет о распределении масс. Мы пока не рассматривали распределения масс, а занимались только отдельными частицами. Но интересно рассчитать и поля, образуемые более чем одной частицей. Для начала найдем силу притяжения со стороны плоско го пласта вещества бесконечнойпротяженности. Сила притяжения единичной массы в данной точке Р (фиг. 13.5), конечно, направлена к плоскости. Расстояние от точки до плоскости есть а, а масса единицы площади этой плоскости есть μ. Пусть |х будет постоянной: слой однороден. Какой же величины поле dC создается массой dm, удаленной от О не ближе, чем на p, и не дальше, чем на p+ dp (О — это точка плоскости, ближайшая к Р)? Ответ: dC = G(dmr/r3). Но оно, это поле, направлено вдоль r, а мы понимаем, что из трех составляющих С после сложения всех dC должна остаться лишь x-составляющая. Она равна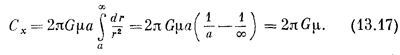
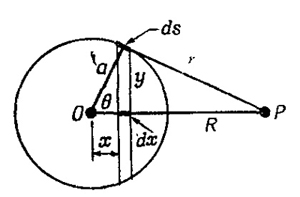 Мы теперь покажем, что это чудо обыкновенное; чтобы продемонстрировать это, разобьем Землю на тонкие сферические слои. Пусть вся масса сферы равна m. Давайте рассчитаем потенциальную энергию частицы массы m` на расстоянии R от центра сферы (фиг. 13.6). Мы увидим, что потенциальная энергия как раз такая, как если бы масса m сферы вся собралась в ее центре. (Легче иметь дело с потенциальной энергией, чем с напряженностью поля: не нужно думать об углах, а просто складывать потенциальные энергии всех частей сферы.) Нарежем сферу на узкие пояски, и пусть х — расстояние плоскости пояска от центра сферы; тогда вся масса пояска толщиной dx находится на одном и том же расстоянии r от точки Р, а потенциальная энергия притяжения этого пояска равна —Gm`dm/r. Сколько же массы содержится в пояске dx? Вот сколько:
Мы теперь покажем, что это чудо обыкновенное; чтобы продемонстрировать это, разобьем Землю на тонкие сферические слои. Пусть вся масса сферы равна m. Давайте рассчитаем потенциальную энергию частицы массы m` на расстоянии R от центра сферы (фиг. 13.6). Мы увидим, что потенциальная энергия как раз такая, как если бы масса m сферы вся собралась в ее центре. (Легче иметь дело с потенциальной энергией, чем с напряженностью поля: не нужно думать об углах, а просто складывать потенциальные энергии всех частей сферы.) Нарежем сферу на узкие пояски, и пусть х — расстояние плоскости пояска от центра сферы; тогда вся масса пояска толщиной dx находится на одном и том же расстоянии r от точки Р, а потенциальная энергия притяжения этого пояска равна —Gm`dm/r. Сколько же массы содержится в пояске dx? Вот сколько: